1217. Minimum Cost to Move Chips to The Same Position

Description

We have n chips, where the position of the i^th chip is position[i].

We need to move all the chips to the same position. In one step, we can change the position of the i^th chip from position[i] to:

• position[i] + 2 or position[i] - 2 with cost = 0.
• position[i] + 1 or position[i] - 1 with cost = 1.

Return the minimum cost needed to move all the chips to the same position.

Example 1:

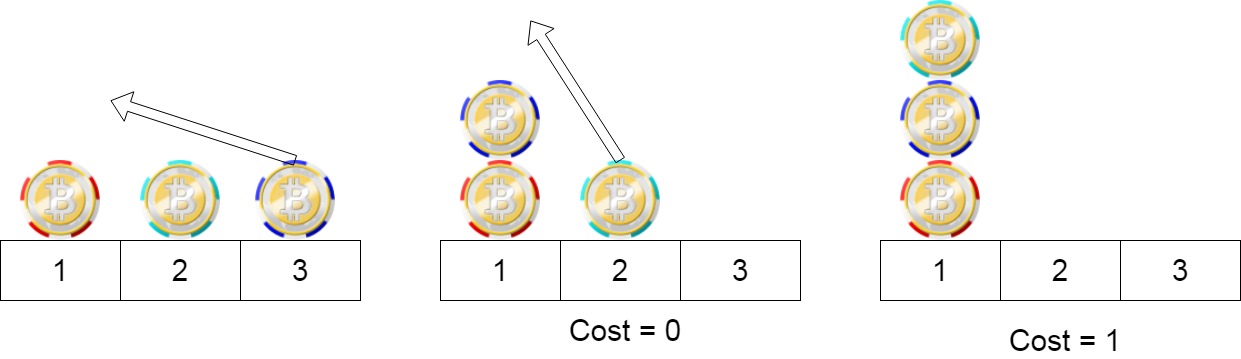
• Input: position = [1,2,3]
• Output: 1
• Explanation: First step: Move the chip at position 3 to position 1 with cost = 0. Second step: Move the chip at position 2 to position 1 with cost = 1. Total cost is 1.

Example 2:

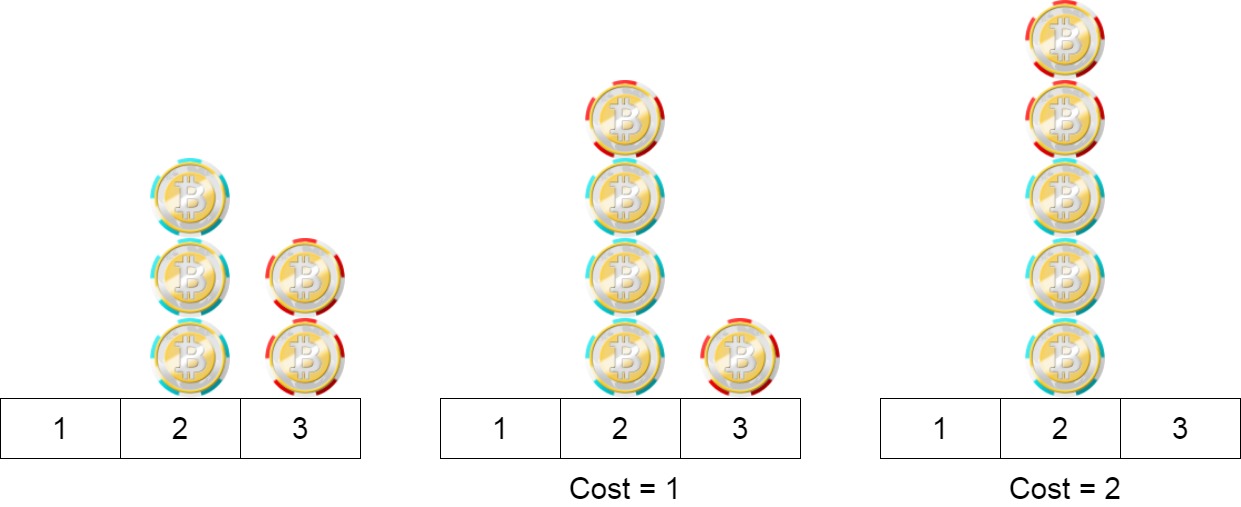
• Input: position = [2,2,2,3,3]
• Output: 2
• Explanation:
  We can move the two chips at position 3 to position 2.
  Each move has cost = 1. The total cost = 2.

Example 3:

• Input: position = [1,1000000000]
• Output: 1

Constraints:

• 1 <= position.length <= 100
• 1 <= position[i] <= 10⁹

💡 Hint 1:
The first move keeps the parity of the element as it is.

💡 Hint 2:
The second move changes the parity of the element.

💡 Hint 3:
Since the first move is free, if all the numbers have the same parity, the answer would be zero.

💡 Hint 4:
Find the minimum cost to make all the numbers have the same parity.

Submitted Code

class Solution:
    def minCostToMoveChips(self, position: List[int]) -> int:
        even_nums, odd_nums = 0, 0

        for n in position:
            if n % 2 == 0:
                even_nums += 1
            else:
                odd_nums += 1
        
        return min(even_nums, odd_nums)

Runtime: 0 ms | Beats 100.00%
Memory: 19.28 MB | Beats 21.46%

짝수 간격으로는 얼마든지 0 코스트로 이동할 수 있고 패리티를 바꾸는 순간에만 비용이 들기 때문에 짝수와 홀수 중 개수가 더 많은 쪽으로 이동하면 된다.

Other Solutions

1st

def minCostToMoveChips(self, chips: List[int]) -> int:
	odds = sum(x % 2 for x in chips)
	return min(odds, len(chips) - odds)

time complexity: 𝑂(𝑛)
space complexity: 𝑂(1)