1232. Check If It Is a Straight Line

Description

You are given an integer array coordinates, coordinates[i] = [x, y], where [x, y] represents the coordinate of a point. Check if these points make a straight line in the XY plane.

Example 1:

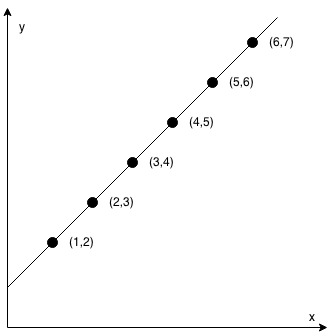
• Input: coordinates = [[1,2],[2,3],[3,4],[4,5],[5,6],[6,7]]
• Output: true

Example 2:

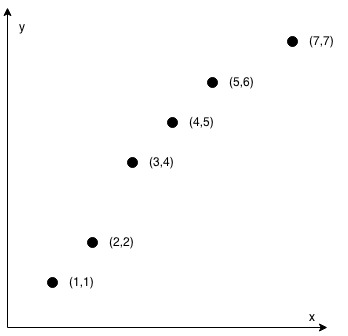
• Input: coordinates = [[1,1],[2,2],[3,4],[4,5],[5,6],[7,7]]
• Output: false

Constraints:

• 2 <= coordinates.length <= 1000
• coordinates[i].length == 2
• -10⁴ <= coordinates[i][0], coordinates[i][1] <= 10⁴
• coordinates contains no duplicate point.

💡 Hint 1:
If there're only 2 points, return true.

💡 Hint 2:
Check if all other points lie on the line defined by the first 2 points.

💡 Hint 3:
Use cross product to check collinearity.

Submitted Code

class Solution:
    def checkStraightLine(self, coordinates: List[List[int]]) -> bool:
        p1 = coordinates[0]                                                 # 기준점(1번째 점)
        v1 = ( (coordinates[1][0] - p1[0]), (coordinates[1][1] - p1[1]) )   # 기준 벡터 p1->p2

        for c in coordinates[2:]:
            v2 = ( (c[0] - p1[0]), (c[1] - p1[1]) )     # 방향 벡터 p1->p3, p1->p4, p1->p5, ...
            if (v1[0] * v2[1]) - (v1[1] * v2[0]) != 0:  # 2차원 외적(cross product)이 0이 아니면 false
                return False

        return True

Runtime: 0 ms | Beats 100.00%
Memory: 19.60 MB | Beats 11.79%

기준점(1번째 점 p1)과 다른 점들 사이의 벡터들이 서로 평행하다면 모든 점이 일직선상에 있다는 의미이다. 때문에 두 벡터가 평행할 경우 교차곱(외적)의 결과값이 0이 된다는 성질을 이용하여 알아낼 수 있다.

Other Solutions

1st

class Solution:
    def checkStraightLine(self, coordinates: List[List[int]]) -> bool:
        (x0, y0), (x1, y1) = coordinates[: 2]
        return all((x1 - x0) * (y - y1) == (x - x1) * (y1 - y0) for x, y in coordinates)

time complexity: 𝑂(𝑛)
space complexity: 𝑂(1)

세 점 (x0, y0), (x1, y1), (x, y)이 일직선상에 있기 위해서는 기울기가 같아야 한다는 것을 이용한 방법이다.
식 (y1 - y0)/(x1 - x0) = (y - y1)/(x - x1)을 곱셈식으로 변경하면 (y1 - y0)(x - x1) = (x1 - x0)(y - y1)이 된다.