1252. Cells with Odd Values in a Matrix

Description

There is an m x n matrix that is initialized to all 0’s. There is also a 2D array indices where each indices[i] = [r_i, c_i] represents a 0-indexed location to perform some increment operations on the matrix.

For each location indices[i], do both of the following:

1. Increment all the cells on row r_i.
2. Increment all the cells on column c_i.

Given m, n, and indices, return the number of odd-valued cells in the matrix after applying the increment to all locations in indices.

Example 1:

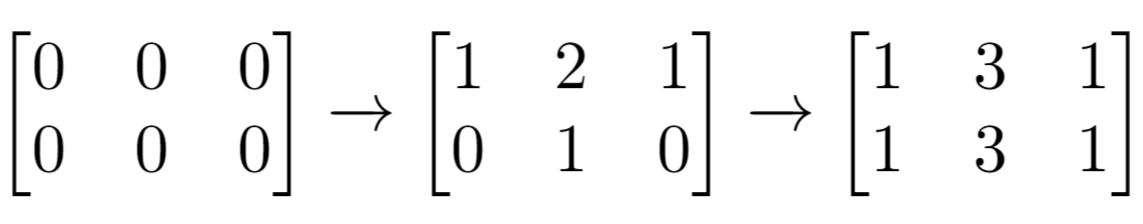
• Input: m = 2, n = 3, indices = [[0,1],[1,1]]
• Output: 6
• Explanation: Initial matrix = [[0,0,0],[0,0,0]].
  After applying first increment it becomes [[1,2,1],[0,1,0]].
  The final matrix is [[1,3,1],[1,3,1]], which contains 6 odd numbers.

Example 2:

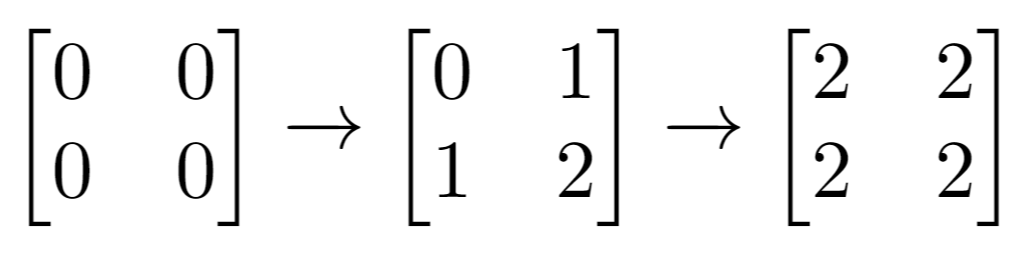
• Input: m = 2, n = 2, indices = [[1,1],[0,0]]
• Output: 0
• Explanation: Final matrix = [[2,2],[2,2]]. There are no odd numbers in the final matrix.

Constraints:

• 1 <= m, n <= 50
• 1 <= indices.length <= 100
• 0 <= r_i < m
• 0 <= c_i < n

Follow up: Could you solve this in O(n + m + indices.length) time with only O(n + m) extra space?

💡 Hint 1:
Simulation : With small constraints, it is possible to apply changes to each row and column and count odd cells after applying it.

💡 Hint 2:
You can accumulate the number you should add to each row and column and then you can count the number of odd cells.

Submitted Code

class Solution:
    def oddCells(self, m: int, n: int, indices: List[List[int]]) -> int:
        rows, cols = [0]*m, [0]*n

        for x,y in indices:                 # O(l)
            rows[x] += 1
            cols[y] += 1

        odd_rows = sum(r % 2 for r in rows) # O(m)
        odd_cols = sum(c % 2 for c in cols) # O(n)

        even_rows = m - odd_rows
        even_cols = n - odd_cols

        return odd_rows * even_cols + even_rows * odd_cols

Runtime: 0 ms | Beats 100.00%
Memory: 19.36 MB | Beats 12.10%

행렬을 이중 for문 루프로 탐색하면 O(n * m + indices.length) 시간이 소요된다. 리트코드 예제는 행렬 크기가 작아서 이렇게 해도 runtime은 0ms로 나오지만 문제에서 요구하는 최적화된 되기 때문에 문제에서 요구하는 최적화된 방법은 아니다. 이 방법은 모든 행과 열을 탐색하지 않고 홀수 행 × 짝수 열 + 짝수 행 × 홀수 열로 빠르게 홀수인 값만 계산할 수 있다.

Other Solutions

1st

    def oddCells(self, n: int, m: int, indices: List[List[int]]) -> int:
        odd_rows, odd_cols, cntRow, cntCol = [False] * n, [False] * m, 0, 0
        for r, c in indices:
            odd_rows[r] ^= True
            odd_cols[c] ^= True
            cntRow += 1 if odd_rows[r] else -1      # 홀수 행 개수 갱신
            cntCol += 1 if odd_cols[c] else -1      # 홀수 열 개수 갱신
        # return m * cntRow + n * cntCol - 2 * cntRow * cntCol
        return (m - cntCol) * cntRow + (n - cntRow) * cntCol

time complexity: 𝑂(𝑚+𝑛+𝓁)
space complexity: 𝑂(𝑚+𝑛)

카운트를 누적하는 대신 각 행과 열의 홀수/짝수 상태만 관리하고 홀수 행/열의 개수도 바로 갱신하는 방법도 있다.