1260. Shift 2D Grid

Description

Given a 2D grid of size m x n and an integer k. You need to shift the grid k times.

In one shift operation:

• Element at grid[i][j] moves to grid[i][j + 1].
• Element at grid[i][n - 1] moves to grid[i + 1][0].
• Element at grid[m - 1][n - 1] moves to grid[0][0].

Return the 2D grid after applying shift operation k times.

Example 1:

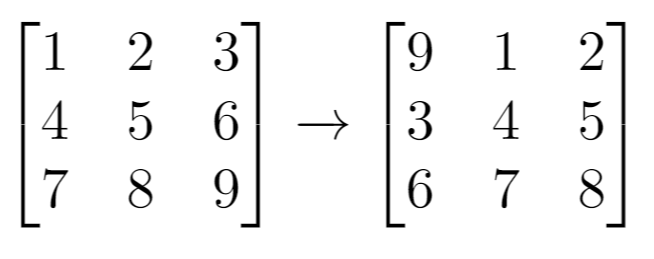
• Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
• Output: [[9,1,2],[3,4,5],[6,7,8]]

Example 2:

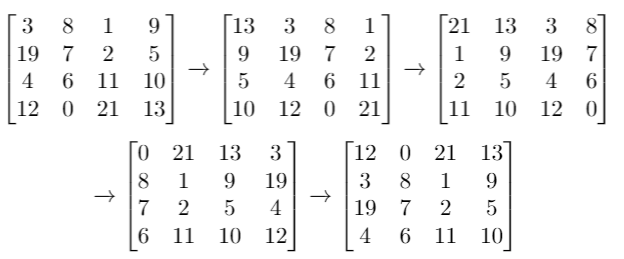
• Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
• Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

Example 3:

• Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
• Output: [[1,2,3],[4,5,6],[7,8,9]]

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m <= 50
• 1 <= n <= 50
• -1000 <= grid[i][j] <= 1000
• 0 <= k <= 100

💡 Hint 1:
Simulate step by step. move grid[i][j] to grid[i][j+1]. handle last column of the grid.

💡 Hint 2:
Put the matrix row by row to a vector. take k % vector.length and move last k of the vector to the beginning. put the vector to the matrix back the same way.

Submitted Code

class Solution:
    def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
        m, n = len(grid), len(grid[0])
        moves = k % (m * n)                 # 완전한 한 바퀴를 모두 돌고 남은 이동 수
        
        if moves == 0:                      # 남은 이동 수가 0이면 바꿀 필요 없음
            return grid

        result = [[0] * n for _ in range(m)]                    # 빈 2차원 리스트 생성
        vector = [cell for row in grid for cell in row]         # 2차원 -> 1차원
        shifted_vector = vector[-moves:] + vector[:-moves]      # moves만큼 뒷부분을 잘라서 앞에 붙임

        for i in range(m * n):
            result[i // n][i % n] = shifted_vector[i]           # 1차원 -> 2차원

        return result

Runtime: 0 ms | Beats 100.00%
Memory: 19.69 MB | Beats 10.62%

2차원 그리드를 1차원으로 펼쳐 오른쪽으로 moves만큼 칸을 이동시킨 뒤, 다시 원래 크기의 2차원 그리드로 재구성하는 방법이다.

Other Solutions

1st

class Solution:
    def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
        nRows, nCols = len(grid), len(grid[0])
        k %= nRows * nCols
        if k == 0: return grid
        n = nRows * nCols
        
        def reverse(grid, left, right):
            while left < right:
                grid[left//nCols][left%nCols], grid[right//nCols][right%nCols] = grid[right//nCols][right%nCols], grid[left//nCols][left%nCols]
                left += 1
                right -= 1

        reverse(grid, 0, n-1)
        reverse(grid, 0, k-1)
        reverse(grid, k, n-1)
        return grid

time complexity: 𝑂(𝑚+𝑛)
space complexity: 𝑂(1)

‘오른쪽으로 k칸 이동’을 배열을 뒤집는 것으로도 구현할 수 있다.

grid = [[1,2,3],[4,5,6],[7,8,9]]
k = 3

[1,2,3,4,5,6,7,8,9]
[9,8,7|6,5,4,3,2,1]  ←  reverse(grid, 0, n-1)
[7,8,9|6,5,4,3,2,1]  ←  reverse(grid, 0, k-1)
[7,8,9|1,2,3,4,5,6]  ←  reverse(grid, k, n-1)
      k

return [[7,8,9],[1,2,3],[4,5,6]]