1266. Minimum Time Visiting All Points

Description

On a 2D plane, there are n points with integer coordinates points[i] = [x_i, y_i]. Return the minimum time in seconds to visit all the points in the order given by points.

You can move according to these rules:

• In 1 second, you can either:
  • move vertically by one unit,
  • move horizontally by one unit, or
  • move diagonally sqrt(2) units (in other words, move one unit vertically then one unit horizontally in 1 second).
• You have to visit the points in the same order as they appear in the array.
• You are allowed to pass through points that appear later in the order, but these do not count as visits.

Example 1:

• Input: points = [[1,1],[3,4],[-1,0]]
• Output: 7
• Explanation:
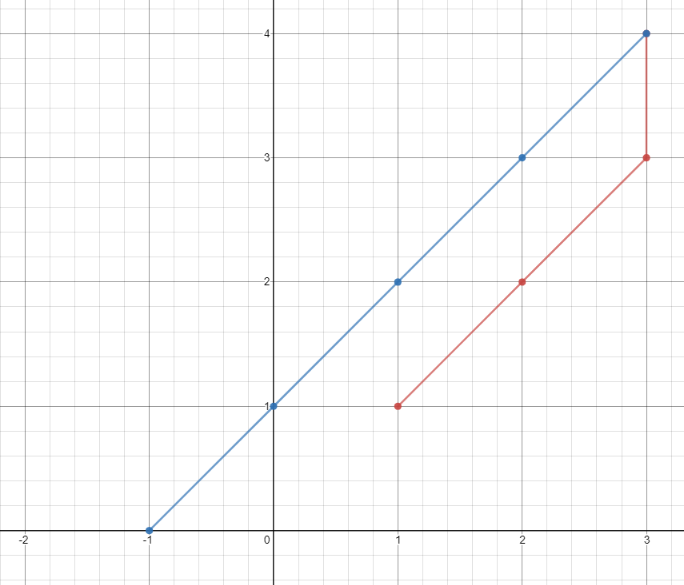
  One optimal path is [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]
  Time from [1,1] to [3,4] = 3 seconds
  Time from [3,4] to [-1,0] = 4 seconds
  Total time = 7 seconds

Example 2:

• Input: points = [[3,2],[-2,2]]
• Output: 5

Constraints:

• points.length == n
• 1 <= n <= 100
• points[i].length == 2
• -1000 <= points[i][0], points[i][1] <= 1000

💡 Hint 1:
To walk from point A to point B there will be an optimal strategy to walk ?

💡 Hint 2:
Advance in diagonal as possible then after that go in straight line.

💡 Hint 3:
Repeat the process until visiting all the points.

Submitted Code

class Solution:
    def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:
        time = 0

        for i in range(len(points)-1):
            dx = abs(points[i+1][0] - points[i][0])
            dy = abs(points[i+1][1] - points[i][1])
            time += max(dx, dy)

        return time

Runtime: 0 ms | Beats 100.00%
Memory: 19.24 MB | Beats 90.20%

dx, dy가 둘 다 남아있는 동안에는 대각선으로 min(dx, dy)번 이동 가능하고 dx, dy가 동시에 1씩 감소된다. 한쪽이 0이 되면 남은 쪽으로 |dx - dy|번 직선 이동하면 된다. 대각선 거리과 직선 거리를 모두 합하면 결국 max(dx, dy)가 된다.

Other Solutions

1st

from itertools import pairwise

class Solution:
    def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:
        return sum(max(abs(P[0]-Q[0]), abs(P[1]-Q[1])) for P, Q in pairwise(points))

time complexity: 𝑂(𝑛)
space complexity: 𝑂(1)

Python 3.10부터 itertools에 추가된 pairwise() 함수로 연속된 원수의 앞과 뒤를 쌍으로 묶을 수 있다. 이하 버전에서는 zip()을 사용하면 된다.
(e.g. [1, 2, 3, 4] → (1, 2), (2, 3), (3, 4))