441. Arranging Coins

Description

You have n coins and you want to build a staircase with these coins. The staircase consists of k rows where the i^th row has exactly i coins. The last row of the staircase may be incomplete.

Given the integer n, return the number of complete rows of the staircase you will build.

Example 1:

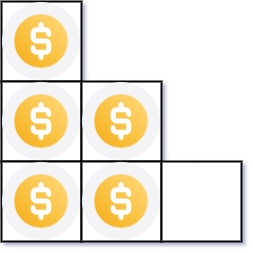
• Input: n = 5
• Output: 2
• Explanation: Because the 3rd row is incomplete, we return 2.

Example 2:

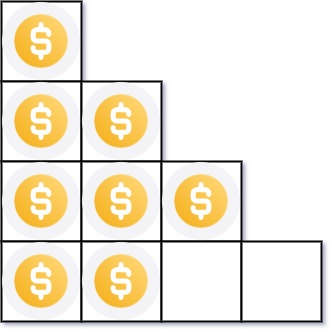
• Input: n = 8
• Output: 3
• Explanation: Because the 4th row is incomplete, we return 3.

Constraints:

• 1 <= n <= 2³¹ - 1

Submitted Code

class Solution(object):
    def arrangeCoins(self, n):
        """
        :type n: int
        :rtype: int
        """
        i = 1
        total = 0

        while total + i < n:
            total += i
            i += 1

        return i if total + i == n else i - 1

1부터 순서대로 한 층씩 더하는 방법은 너무 오래걸린다.

class Solution(object):
    def arrangeCoins(self, n):
        """
        :type n: int
        :rtype: int
        """
        front = 1
        back = n

        while front <= back:
            mid = (front + back) // 2
            total = (mid * (mid+1)) // 2    # 1부터 mid까지의 합

            if total == n or\                         
               total < n and total + (mid + 1) > n:   # total이 n과 같거나, 한 층을 더하면 동전이 부족한 경우
                return mid
            elif total < n:
                front = mid + 1
            else:
                back = mid - 1

Runtime: 0 ms | Beats 100.00%
Memory: 12.53 MB | Beats 8.32%

이진 탐색을 활용한 방법으로, 1부터 k까지의 숫자를 모두 더한 값은 k(k+1) / 2 라는 공식도 함께 사용했다.

Other Solutions

1st

class Solution(object):
    def arrangeCoins(self, n):
        L, R = 0, n
        while L <= R:
            M = (L + R) // 2
            if M * (M + 1) // 2 <= n:
                L = M + 1
            else:
                R = M - 1
        return R    # 조건을 만족하는 최대값 반환

time complexity: 𝑂(log𝑛)
space complexity: 𝑂(1)

이진 탐색을 좀 더 간단하게 할 수 있었다는 것을 알게 되어 참고했다.

2nd

import math

class Solution(object):
    def arrangeCoins(self, n):
        return int((math.sqrt(8 * n + 1) - 1) // 2)

좀 더 수학적으로 접근한 답안이다. k(k+1) / 2 <= n을 만족하는 k를 구하기 위해 이차방정식 k² + k - 2n <= 0 으로 변환한 후, 근의 공식을 사용하여 k = (-1 + √1+8n) / 2 으로 만든다. k의 소수점을 버리고 정수 부분만 취하면 정답이 된다.