563. Binary Tree Tilt

Description

Given the root of a binary tree, return the sum of every tree node’s tilt.

The tilt of a tree node is the absolute difference between the sum of all left subtree node values and all right subtree node values. If a node does not have a left child, then the sum of the left subtree node values is treated as 0. The rule is similar if the node does not have a right child.

Example 1:

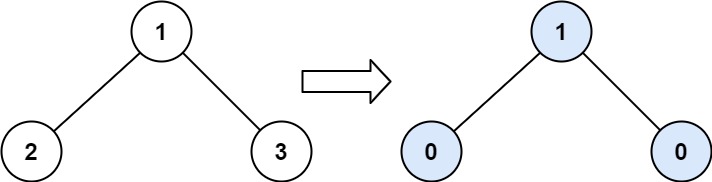
• Input: root = [1,2,3]
• Output: 1
• Explanation:
  • Tilt of node 2 : |0-0| = 0 (no children)
  • Tilt of node 3 : |0-0| = 0 (no children)
  • Tilt of node 1 : |2-3| = 1
    (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3)

Sum of every tilt : 0 + 0 + 1 = 1

Example 2:

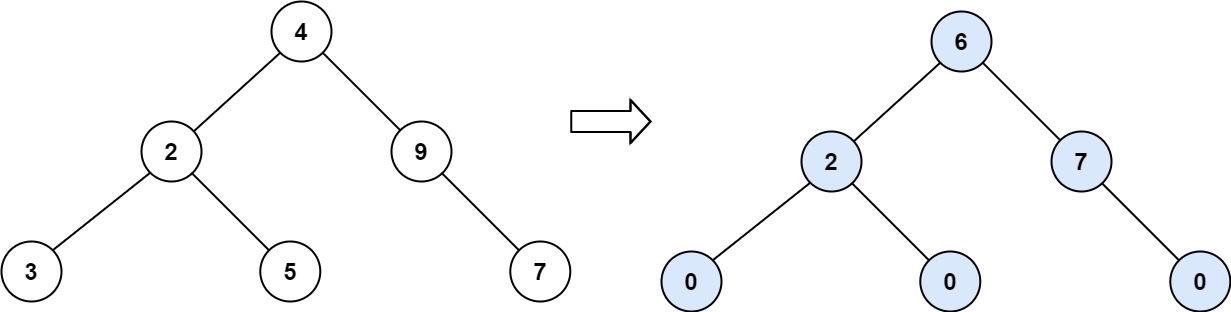
• Input: root = [4,2,9,3,5,null,7]
• Output: 15
• Explanation:
  • Tilt of node 3 : |0-0| = 0 (no children)
  • Tilt of node 5 : |0-0| = 0 (no children)
  • Tilt of node 7 : |0-0| = 0 (no children)
  • Tilt of node 2 : |3-5| = 2
    (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5)
  • Tilt of node 9 : |0-7| = 7
    (no left child, so sum is 0; right subtree is just right child, so sum is 7)
  • Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6
    (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16)

Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15

Example 3:

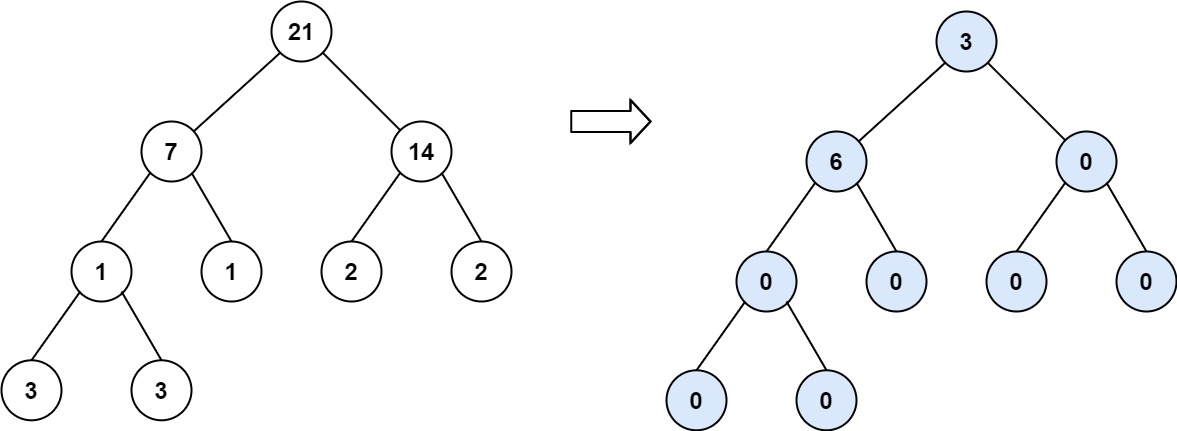
• Input: root = [21,7,14,1,1,2,2,3,3]
• Output: 9

Constraints:

• The number of nodes in the tree is in the range [0, 10⁴].
• -1000 <= Node.val <= 1000

💡 Hint 1:
Don't think too much, this is an easy problem. Take some small tree as an example.

💡 Hint 2:
Can a parent node use the values of its child nodes? How will you implement it?

💡 Hint 3:
May be recursion and tree traversal can help you in implementing.

💡 Hint 4:
What about postorder traversal, using values of left and right childs?

Submitted Code

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution(object):
    def findTilt(self, root):
        """
        :type root: Optional[TreeNode]
        :rtype: int
        """
        self.total_tilt = 0

        def dfs(node):
            if not node:
                return 0

            left_sum = dfs(node.left)
            right_sum = dfs(node.right)

            self.total_tilt += abs(left_sum - right_sum)    # 현재 노드의 tilt 계산
            return node.val + left_sum + right_sum          # 현재 서브트리들의 총합 리턴

        dfs(root)
        return self.total_tilt

Runtime: 5 ms | Beats 80.66%
Memory: 15.36 MB | Beats 41.15%

재귀 호출로 트리를 순회하며 각 노드의 tilt를 누적하고 서브트리의 총합을 구한다.

Other Solutions

1st

class Solution:
    def findTilt(self, root):
        def dfs(node):
            if not node: return [0,0]
            t1, s1 = dfs(node.left)     # tilt, sum of left subtree
            t2, s2 = dfs(node.right)    # tilt, sum of right subtree
            return [t1+t2+abs(s1-s2), s1+s2+node.val]
        return dfs(root)[0]

time complexity: 𝑂(𝑛)
space complexity: 𝑂(ℎ)

같은 원리지만 조금 더 짧은 코드다.