598. Range Addition II

Description

You are given an m x n matrix M initialized with all 0’s and an array of operations ops, where ops[i] = [a_i, b_i] means M[x][y] should be incremented by one for all 0 <= x < a_i and 0 <= y < b_i.

Count and return the number of maximum integers in the matrix after performing all the operations.

Example 1:

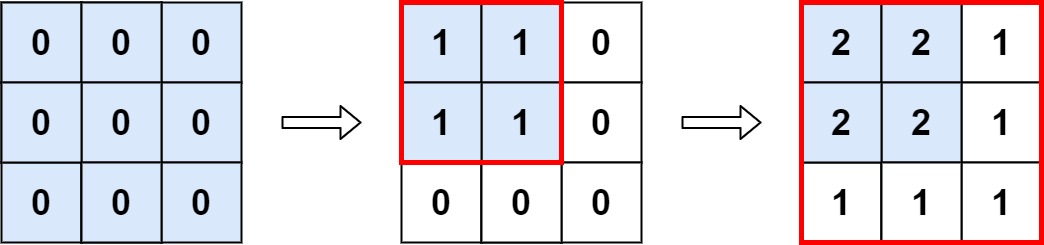
• Input: m = 3, n = 3, ops = [[2,2],[3,3]]
• Output: 4
• Explanation: The maximum integer in M is 2, and there are four of it in M. So return 4.

Example 2:

• Input: m = 3, n = 3, ops = [[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3]]
• Output: 4

Example 3:

• Input: m = 3, n = 3, ops = []
• Output: 9

Constraints:

• 1 <= m, n <= 4 * 10⁴
• 0 <= ops.length <= 10⁴
• ops[i].length == 2
• 1 <= a_i <= m
• 1 <= b_i <= n

Submitted Code

class Solution(object):
    def maxCount(self, m, n, ops):
        """
        :type m: int
        :type n: int
        :type ops: List[List[int]]
        :rtype: int
        """
        if not ops:
            return m * n
        
        matrix = [0] * m * n
        max_num = 0
        
        for o in ops:
            for i in range(o[0]):
                for j in range(o[1]):
                    idx = (i * m) + j
                    matrix[idx] += 1   
            max_num += 1
        
        return matrix.count(max_num)

이 코드로는 시간 복잡도가 너무 높아서 통과하지 못하는 테스트 케이스들이 있었다.

class Solution(object):
    def maxCount(self, m, n, ops):
        if not ops:
            return m * n
        
        min_a = min([op[0] for op in ops])
        min_b = min([op[1] for op in ops])

        return min_a * min_b

Runtime: 0 ms | Beats 100.00%
Memory: 13.47 MB | Beats 57.99%

가장 큰 값이 있는 칸의 개수만 구하면 되기 때문에 간단하게 할 수 있다. ops의 각 원소가 [a, b]일 때, 모든 ops가 영향을 주는 공통 영역은 min(a), min(b)이라는 것을 이용했다.

Other Solutions

1st

class Solution(object):
    def maxCount(self, m, n, ops):
        if not ops:
            return m * n
        min_a = min(op[0] for op in ops)
        min_b = min(op[1] for op in ops)
        return min_a * min_b

time complexity: 𝑂(𝑛) ← len(ops)
space complexity: 𝑂(1)

리스트 컴프리헨션이 아니라 min(op[0] for op in ops) 처럼 제너레이터 표현식을 사용해도 된다.

2nd

class Solution:
    def maxCount(self, m: int, n: int, ops: List[List[int]]) -> int:
        if not ops: return m * n
        min_a, min_b = m, n
        for a, b in ops:
            if a < min_a: min_a = a
            if b < min_b: min_b = b
        return min_a * min_b

위의 코드를 min() 함수 없이 조건문으로 풀어서 쓸 수도 있다.