812. Largest Triangle Area

Description

Given an array of points on the X-Y plane points where points[i] = [x_i, y_i], return the area of the largest triangle that can be formed by any three different points. Answers within 10^-5 of the actual answer will be accepted.

Example 1:

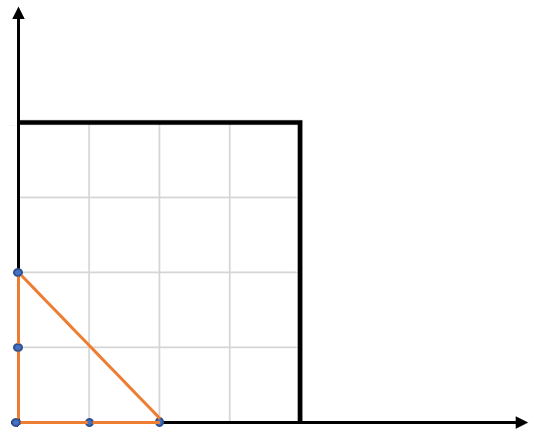
• Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
• Output: 2.00000
• Explanation: The five points are shown in the above figure. The red triangle is the largest.

Example 2:

• Input: points = [[1,0],[0,0],[0,1]]
• Output: 0.50000

Constraints:

• 3 <= points.length <= 50
• -50 <= xi, yi <= 50
• All the given points are unique.

Submitted Code

class Solution(object):
    def largestTriangleArea(self, points):
        """
        :type points: List[List[int]]
        :rtype: float
        """
        n = len(points)
        max_area = 0

        for i in range(n):
            for j in range(i+1, n):
                for k in range(j+1, n):
                    x1, y1 = points[i]
                    x2, y2 = points[j]
                    x3, y3 = points[k]

                    area = abs(x1*y2 + x2*y3 + x3*y1 - x2*y1 - x3*y2 - x1*y3) * 0.5
                    max_area = max(max_area, area)

        return max_area

Runtime: 59 ms | Beats 46.90%
Memory: 12.37 MB | Beats 84.83%

브루트포스로 가능한 모든 세 점 조합을 뽑은 후, 각 조합에 아래의 신발끈 공식(가우스의 면적 공식)을 적용시켜 삼각형의 넓이를 구했다.

Other Solutions

1st

class Solution:
    def largestTriangleArea(self, points: List[List[int]]) -> float:
        return max(abs(0.5*(x1*(y2-y3)+x2*(y3-y1)+x3*(y1-y2))) for [x1,y1], [x2,y2], [x3,y3] in combinations(points, 3))

time complexity: 𝑂(𝑛³)
space complexity: 𝑂(1)

파이썬 내장 라이브러리 itertools.combinations로 가능한 모든 3개 조합을 중복없이 뽑을 수 있다.
여기서는 벡터 외적 공식으로 삼각형의 넓이를 구했다.