883. Projection Area of 3D Shapes

Description

You are given an n x n grid where we place some 1 x 1 x 1 cubes that are axis-aligned with the x, y, and z axes.

Each value v = grid[i][j] represents a tower of v cubes placed on top of the cell (i, j).

We view the projection of these cubes onto the xy, yz, and zx planes.

A projection is like a shadow, that maps our 3-dimensional figure to a 2-dimensional plane. We are viewing the “shadow” when looking at the cubes from the top, the front, and the side.

Return the total area of all three projections.

Example 1:

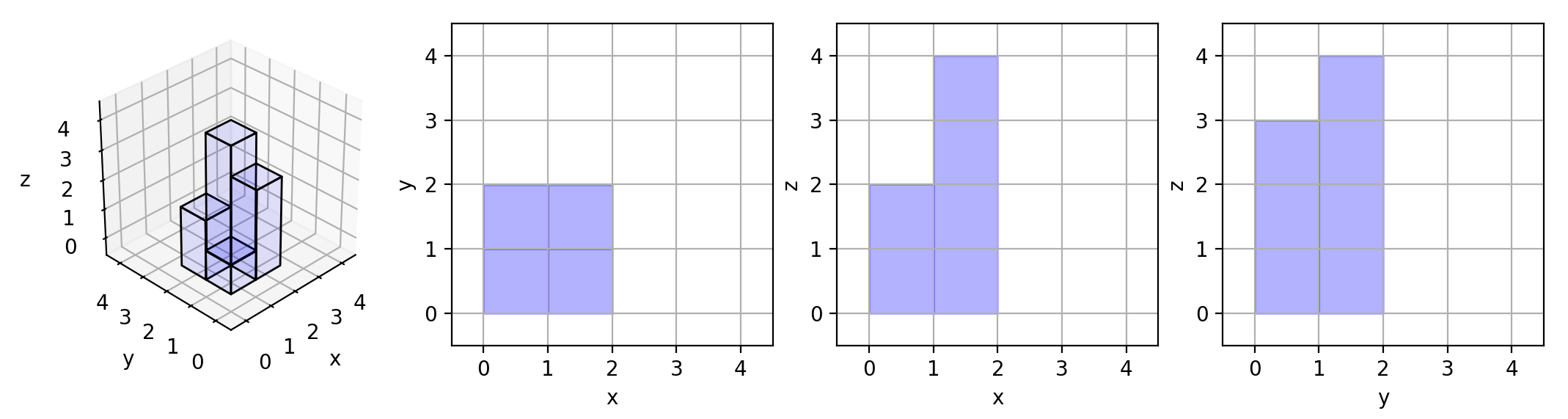
• Input: grid = [[1,2],[3,4]]
• Output: 17
• Explanation: Here are the three projections (“shadows”) of the shape made with each axis-aligned plane.

Example 2:

• Input: grid = [[2]]
• Output: 5

Example 3:

• Input: grid = [[1,0],[0,2]]
• Output: 8

Constraints:

• n == grid.length == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] <= 50

Submitted Code

class Solution(object):
    def projectionArea(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        n = len(grid)
        top, hor, ver = 0, 0, 0   # 윗면(xy), 옆면(zx), 앞면(zy)

        for i in range(n):
            row_max, col_max = 0, 0
            for j in range(n):
                top += 1 if grid[i][j] > 0 else 0     # 0보다 큰 셀의 개수
                row_max = max(grid[i][j], row_max)    # 각 행의 최댓값들의 합
                col_max = max(grid[j][i], col_max)    # 각 열의 최댓값들의 합
            hor += row_max
            ver += col_max

        return top + hor + ver

Runtime: 3 ms | Beats 76.60%
Memory: 12.44 MB | Beats 67.02%

행과 열의 길이가 똑같은 행렬이기 때문에 행과 열의 인덱스를 서로 바꿔주기만 하면 한 행이나 열에서 최댓값을 찾을 수 있다.

Other Solutions

1st

class Solution(object):
    def projectionArea(self, grid):
        hor = sum(map(max, grid))                     # 각 행의 최대값들의 합
        ver = sum(map(max, zip(*grid)))               # 각 열의 최대값들의 합
        top = sum(v > 0 for row in grid for v in row) # xy 평면의 면적
        return ver + hor + top

class Solution(object):
    def projectionArea(self, grid):
        return sum(map(max, grid + zip(*grid))) + sum(v > 0 for row in grid for v in row)

time complexity: 𝑂(𝑛²)
space complexity: 𝑂(1)

같은 원리이지만 좀 더 파이썬스럽게 작성된 코드를 참고했다. zip(*grid)에서 언패킹 연산자 *가 들어간 *grid는 리스트를 풀어서 인자로 전달하고, zip()으로 각 열 단위를 튜플로 묶어준다.