892. Surface Area of 3D Shapes

Description

You are given an n x n grid where you have placed some 1 x 1 x 1 cubes. Each value v = grid[i][j] represents a tower of v cubes placed on top of cell (i, j).

After placing these cubes, you have decided to glue any directly adjacent cubes to each other, forming several irregular 3D shapes.

Return the total surface area of the resulting shapes.

Note: The bottom face of each shape counts toward its surface area.

Example 1:

• Input: grid = [[1,2],[3,4]]
• Output: 34

Example 2:

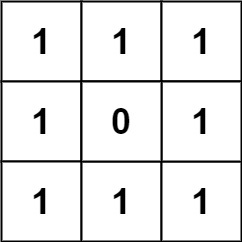
• Input: grid = [[1,1,1],[1,0,1],[1,1,1]]
• Output: 32

Example 3:

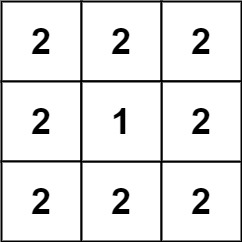
• Input: grid = [[2,2,2],[2,1,2],[2,2,2]]
• Output: 46

Constraints:

• n == grid.length == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] <= 50

Submitted Code

class Solution(object):
    def surfaceArea(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        n = len(grid)
        surface = 0

        for i in range(n):
            for j in range(n):
                if grid[i][j] > 0:               # 해당 셀에 큐브가 있을 때만 면적 계산
                    surface += 6 * grid[i][j]    # 한 큐브의 면적 6 * 쌓인 큐브 개수

                    # 큐브끼리 맞닿은 면 빼기
                    surface -= 2 * (grid[i][j] - 1)                  # 쌓인 큐브끼리 인접면
                    if i > 0:
                        surface -= 2 * min(grid[i][j], grid[i-1][j]) # 위아래 큐브끼리 인접면
                    if j > 0:
                        surface -= 2 * min(grid[i][j], grid[i][j-1]) # 양옆 큐브끼리 인접면

        return surface

Runtime: 9 ms | Beats 81.33%
Memory: 12.43 MB | Beats 72.00%

한 큐브 당 면적을 6으로 계산한 뒤, 다른 큐브와 인접한 부분을 빼는 방법이다.

Other Solutions

1st

class Solution(object):
    def surfaceArea(self, grid):
        n, res = len(grid), 0
        for i in range(n):
            for j in range(n):
                if grid[i][j]: res += 2 + grid[i][j] * 4
                if i: res -= min(grid[i][j], grid[i - 1][j]) * 2
                if j: res -= min(grid[i][j], grid[i][j - 1]) * 2
        return res

class Solution(object):
    def surfaceArea(self, grid):
        return sum(v * 4 + 2 for row in grid for v in row if v) - sum(min(a, b) * 2 for row in grid + zip(*grid) for a, b in zip(row, row[1:]))

time complexity: 𝑂(𝑛²)
space complexity: 𝑂(1)

조금 더 간단하게 작성된 코드이다.