897. Increasing Order Search Tree

Description

Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.

Example 1:

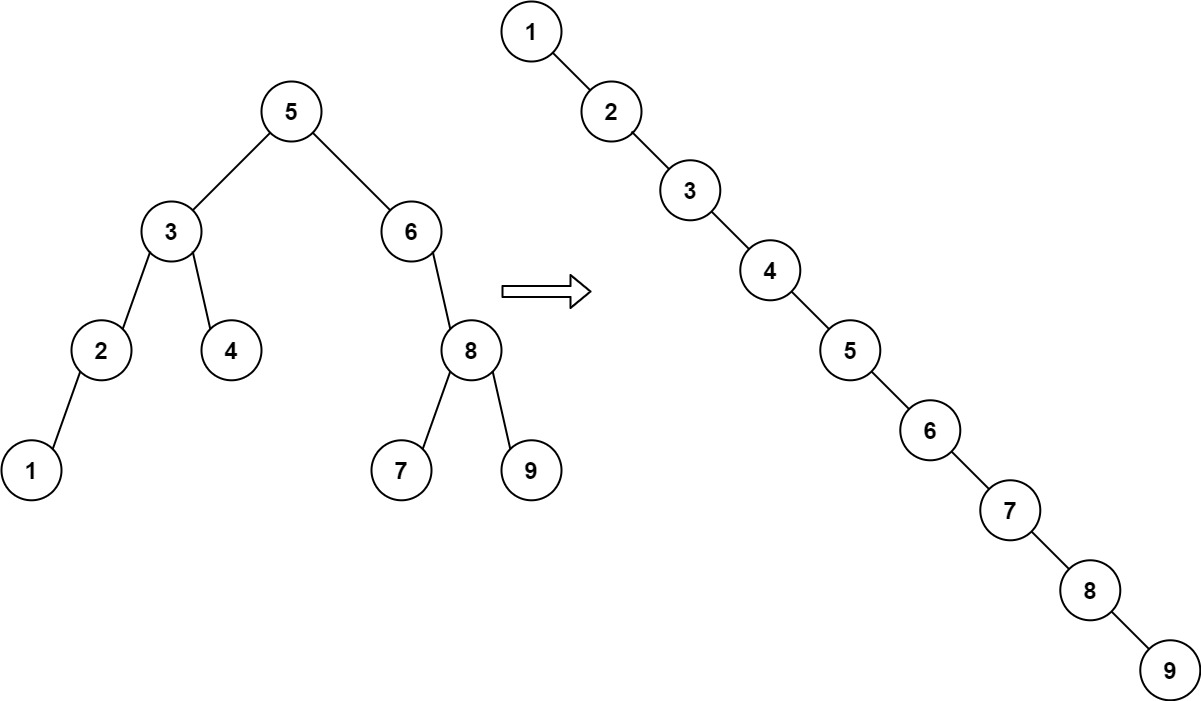
• Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
• Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

Example 2:

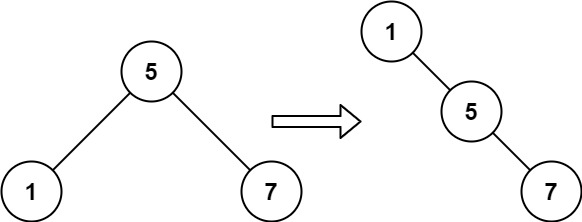
• Input: root = [5,1,7]
• Output: [1,null,5,null,7]

Constraints:

• The number of nodes in the given tree will be in the range [1, 100].
• 0 <= Node.val <= 1000

Submitted Code

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution(object):
    def increasingBST(self, root):
        """
        :type root: Optional[TreeNode]
        :rtype: Optional[TreeNode]
        """
        dummy = TreeNode(0)             # 더미 노드를 헤드로 하는 새 트리 생성
        self.curr = dummy               # 현재 연결 위치

        def inorder(node):
            if not node:
                return

            inorder(node.left)          # 왼쪽 서브트리 먼저 방문
            node.left = None                # 해당 노드의 왼쪽 연결 끊기
            self.curr.right = node          # 현재 노드를 오른쪽 자식으로 연결
            self.curr = node                # 포인터 위치 변경
            inorder(node.right)         # 오른쪽 서브트리 방문

        inorder(root)
        return dummy.right              # 더미 노드 오른쪽 자식 반환

Runtime: 0 ms | Beats 100.00%
Memory: 12.44 MB | Beats 78.77%

Other Solutions

1st

class Solution:
    def increasingBST(self, root):
        def dfs(node):
            l1, r2 = node, node         # 기본값은 잎노드로 가정
            
            if node.left: 
                l1, l2 = dfs(node.left)
                l2.right = node
                
            if node.right:
                r1, r2 = dfs(node.right)
                node.right = r1
            
            node.left = None
            return (l1, r2)
        
        return dfs(root)[0]

time complexity: 𝑂(𝑛)
space complexity: 𝑂(ℎ)

node를 루트로 하는 서브트리를 오른쪽으로만 이어지는 형태로 변경한 뒤, 그 트리의 가장 왼쪽 노드 l1와 가장 오른쪽 노드 r2를 반환하는 구조다.

2nd

class Solution: 
    def increasingBST(self, root, tail = None):
        if not root: return tail
        res = self.increasingBST(root.left, root)
        root.left = None
        root.right = self.increasingBST(root.right, tail)
        return res

이 코드는 포인터 변수 없이 매개변수 tail을 이용해서 현재 서브트리의 다음 노드(꼬리)를 전달하는 형태다.