938. Range Sum of BST

Description

Given the root node of a binary search tree and two integers low and high, return the sum of values of all nodes with a value in the inclusive range [low, high].

Example 1:

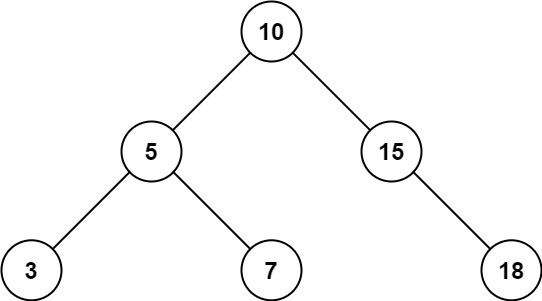
• Input: root = [10,5,15,3,7,null,18], low = 7, high = 15
• Output: 32
• Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.

Example 2:

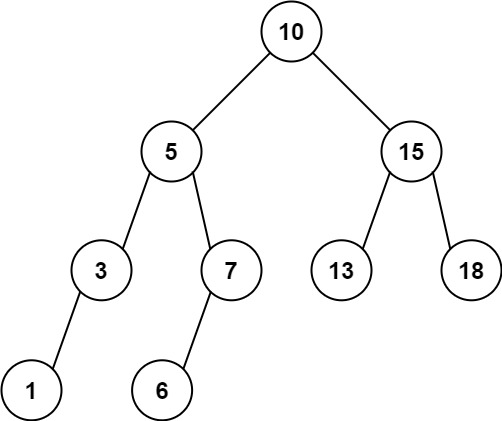
• Input: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
• Output: 23
• Explanation: Nodes 6, 7, and 10 are in the range [6, 10]. 6 + 7 + 10 = 23.

Constraints:

• The number of nodes in the tree is in the range [1, 2 * 10⁴].
• 1 <= Node.val <= 10⁵
• 1 <= low <= high <= 10⁵
• All Node.val are unique.

Submitted Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
        self.total = 0

        def dfs(node):
            if not node:
                return
            
            if low <= node.val <= high:   # 현재 노드값이 범위에 포함되면 합계에 더하기
                self.total += node.val

            if node.val > low:            # 현재 노드값이 범위 최소값보다 클 때만 왼쪽 노드 탐색
                dfs(node.left)
            if node.val < high:           # 현재 노드값이 범위 최대값보다 작을 때만 오른쪽 노드 탐색
                dfs(node.right)
        
        dfs(root)
        return self.total

Runtime: 0 ms | Beats 100.00%
Memory: 25.08 MB | Beats 87.81%

이진 탐색 트리의 특성을 이용하면 모든 노드를 탐색하지 않아도 된다.

Other Solutions

1st

class Solution:
    def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
        if not root:
            return 0
        
        if root.val < low:
            return self.rangeSumBST(root.right, low, high)
        if root.val > high:
            return self.rangeSumBST(root.left, low, high)
        
        return root.val + self.rangeSumBST(root.left, low, high) + self.rangeSumBST(root.right, low, high)

time complexity: 𝑂(𝑛)
space complexity: 𝑂(ℎ)

인스턴스 변수나 내부의 또 다른 함수 없이도 풀 수 있다.