94. Binary Tree Inorder Traversal

Description

Given the root of a binary tree, return the inorder traversal of its nodes’ values.

Example 1:

• Input: root = [1,null,2,3]
• Output: [1,3,2]
• Explanation:

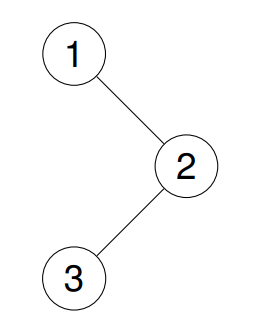
Example 2:

• Input: root = [1,2,3,4,5,null,8,null,null,6,7,9]
• Output: [4,2,6,5,7,1,3,9,8]
• Explanation:

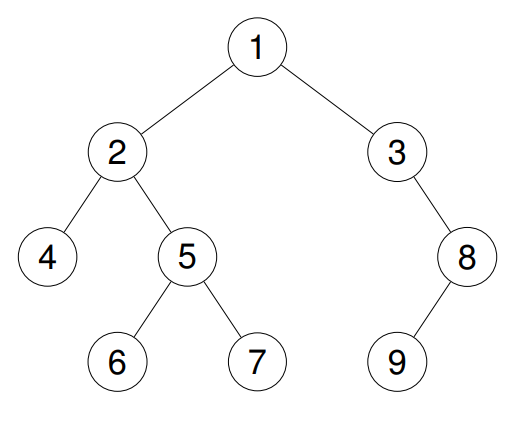
Example 3:

• Input: root = []
• Output: []

Example 4:

• Input: root = [1]
• Output: [1]

Constraints:

• The number of nodes in the tree is in the range [0, 100].
• -100 <= Node.val <= 100

Follow up: Recursive solution is trivial, could you do it iteratively?

Submitted Code

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution(object):
    def inorderTraversal(self, root):
        """
        :type root: Optional[TreeNode]
        :rtype: List[int]
        """
        def traverse(node, result):           # 재귀호출로 중위순회를 하는 함수
            if node is not None:              # null로 입력받은 노드를 출력해보면 None 값을 가짐
                traverse(node.left, result)   # 왼쪽 서브트리 방문
                result.append(node.val)       # 현재 노드 값 추가
                traverse(node.right, result)  # 오른쪽 서브트리 방문

        result = []
        traverse(root, result)
        return result

Runtime: 3 ms | Beats 3.88%
Memory: 12.47 MB | Beats 36.88%

재귀 호출을 사용했다. result에 값을 계속 저장하기 위해 재귀 호출하는 함수를 따로 만들어야 했다. 효율이 좋은 방식은 아니지만 이진 트리를 파이썬으로 구현하는 방법이 익숙하지 않아서 구조 이해를 목표로 했다.

root = [1,null,2,3]

  1
 / \
n   2
   / \
  3   n

traverse(root=TreeNode(1), result=[])
  ↳
  traverse(node.left=None, result=[])
    ↳
    traverse(node=None, result=[])
    ↓
    아무 작업 없이 리턴
  ↓
  result.append(1)
  ↓
  traverse(node.right=TreeNode(2), result=[1])
    ↳ 
    traverse(node=TreeNode(2), result=[1])
      ↳ 
      traverse(node.left=TreeNode(3), result=[1])
        ↳
        traverse(node=TreeNode(3), result=[1])
          ↳
          traverse(node.left=None, result=[1])
            ↳
            traverse(node=None, result=[1])
            ↓
            아무 작업 없이 리턴
          ↓
          result.append(3)
          ↓
          traverse(node.right=None, result=[1, 3])
            ↳
            traverse(node=None, result=[1, 3])
            ↓
            아무 작업 없이 리턴
      ↓
      result.append(2)
      ↓ 
      traverse(node.right=None, result=[1, 3, 2])
        ↳
        traverse(node=None, result=[1, 3, 2])
        ↓
        아무 작업 없이 리턴

result= [1,3,2]

Other Solutions

1st

class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        res = []      # 결과 저장 리스트
        stack = []    # 스택 리스트
        
        while root or stack:        # root가 None이고 스택도 비었으면(더이상 노드가 없음) 종료
            while root:               # 현재 root가 None이면 종료
                stack.append(root)      # 노드를 스택에 저장
                root = root.left        # 현재 root를 왼쪽 자식으로 이동

            root = stack.pop()        # 스택에서 노드를 꺼내서 현재 노드를 처리
            res.append(root.val)      # 꺼낸 노드의 값을 결과에 추가
            root = root.right         # 현재 root를 오른쪽 자식으로 이동
        
        return res

time complexity: 𝑂(𝑛)
space complexity: 𝑂(𝑛)

스택으로 중위 순회를 구현하는 답안이다. 시간 복잡도와 공간 복잡도는 재귀 호출 방식과 같지만, 트리의 크기가 커지면 생길 수 있는 오버헤드가 문제가 없기 때문에 훨씬 더 효율적이었다.

2nd

class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:

        # If the current node is None (base case), return an empty list
        if not root:
            return []
        
        # Recursively get the inorder traversal of the left subtree
        left_tree = self.inorderTraversal(root.left)
        
        # Recursively get the inorder traversal of the right subtree
        right_tree = self.inorderTraversal(root.right)
        
        # Combine the results: left subtree values, current node value, and right subtree values
        return left_tree + [root.val] + right_tree

제출했던 코드보다 더 간결하고 이해가 쉬운 답안이어서 참고했다.

root = [1,null,2,3]

  1
 / \
n   2
   / \
  3   n

root = 1  →  [] + [1] + [우측 순회]
root = 2  →             [좌측 순회]
root = 3  →             []+[3]+[]
root = 2  →                [3]   + [2] + []
root = 1  →  [] + [1] +         [3, 2]

result= [1,3,2]