941. Valid Mountain Array

Description

Given an array of integers arr, return true if and only if it is a valid mountain array.

Recall that arr is a mountain array if and only if:

• arr.length >= 3
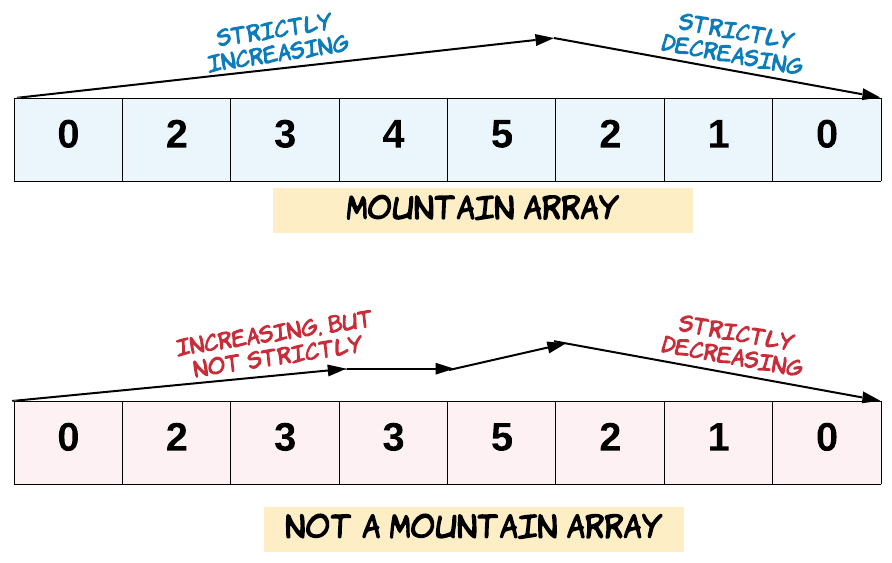
• There exists some i with 0 < i < arr.length - 1 such that:
  • arr[0] < arr[1] < ... < arr[i - 1] < arr[i]
  • arr[i] > arr[i + 1] > ... > arr[arr.length - 1]

Example 1:

• Input: arr = [2,1]
• Output: false

Example 2:

• Input: arr = [3,5,5]
• Output: false

Example 3:

• Input: arr = [0,3,2,1]
• Output: true

Constraints:

• 1 <= arr.length <= 10⁴
• 0 <= arr[i] <= 10⁴

💡 Hint 1:
It's very easy to keep track of a monotonically increasing or decreasing ordering of elements. You just need to be able to determine the start of the valley in the mountain and from that point onwards, it should be a valley i.e. no mini-hills after that. Use this information in regards to the values in the array and you will be able to come up with a straightforward solution.

Submitted Code

class Solution:
    def validMountainArray(self, arr: List[int]) -> bool:
        top, is_down = 0, False                 # 산 정상 인덱스, 현재 하산 중인지 확인

        for i in range(1, len(arr)):
            diff = arr[i] - arr[i-1]            # 현재값과 이전값의 차이

            if diff == 0:                       # 평지 -> false
                return False

            if not is_down:                     # 등산 중인 상태일 경우
                if diff < 0:                        # diff가 음수이면 하산하기 시작한 것
                    if top == 0:                        # 등산 없이 하산만 하는 경우 -> false
                        return False
                    is_down = True
                else:                               # diff가 양수이면 top 위치 갱신
                    top = i
            else:                               # 하산 중인 상태일 경우
                if diff > 0:
                    return False
            
        return top != 0 and is_down             # arr 길이가 1이거나, 하산 없이 등산만 한 경우 -> false

Runtime: 160 ms | Beats 74.63%
Memory: 19.41 MB | Beats 19.06%

top이 0이면 [8,7,6]과 같이 하강만 하거나 [2]처럼 길이가 1인 경우이고, is_down이 false일 경우 [1,2,3]과 같이 상승만 하는 케이스다.

Other Solutions

1st

class Solution:
    def validMountainArray(self, A):
        i, j, n = 0, len(A) - 1, len(A)
        while i + 1 < n and A[i] < A[i + 1]:
          i += 1
        while j > 0 and A[j - 1] > A[j]:
          j -= 1
        return 0 < i == j < n - 1

time complexity: 𝑂(𝑛)
space complexity: 𝑂(1)

올라가는 단계와 내려가는 단계를 나누어서 순회하는 코드가 더 가독성이 좋은 것 같다. 앞에서부터 올라가는 포인터 i와 뒤에서부터 올라가는 포인터 j를 이동시켜서 두 포인터가 같은 곳(정상)에서 만나야 하고, 정상은 맨 처음이나 끝이 아니어야 한다는 것을 간략하게 나타낼 수 있다.